处理量子扰动中的收益递减GydF4y2Ba
对于许多物理学家来说,有一个持久的愿望以最重要的方式解释宇宙的基本构建块。目前,最广泛接受的做法是一个名为“量子场理论”(QFT)的理论框架。该数学工具集中而不是以我们通常想到的方式成为有形的球体,而是将子颗粒视为潜在量子场的激动状态。这个想法最终得到了标准模型:现在形成粒子物理学的基础的理论。GydF4y2Ba
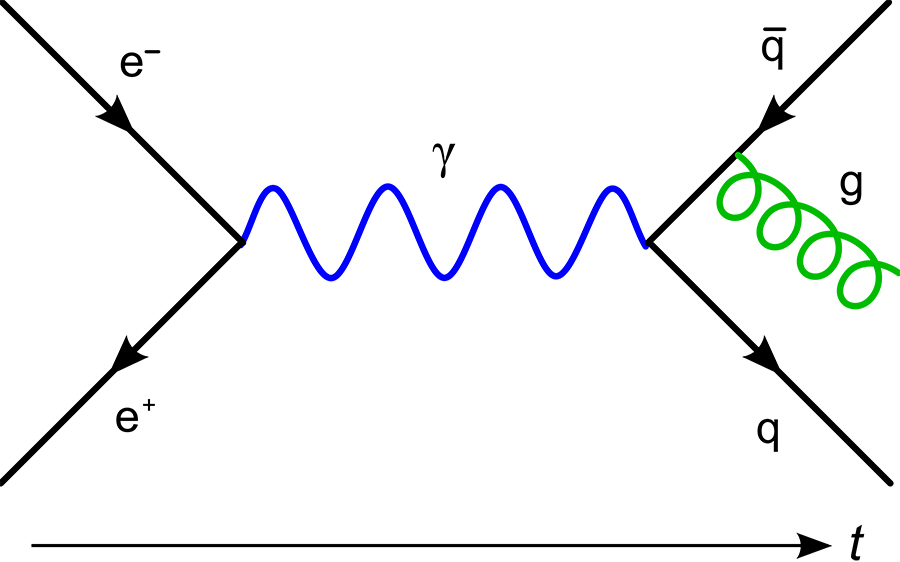
1948年,庆祝物理学家Richard Feynman设计了一种巧妙的方式来可视化QFT中涉及的深层复杂数学。在他现在的着名图中,粒子的路径描绘为线,在它们与其他颗粒相互作用时结束或改变课程。例如,如果两种具有相反电荷的粒子相遇,它们会互相排斥 - 但它们必须以一种节省整体矩的方式这样做。根据QFT,通过通过光子交换动力来实现这一点,在FEYNMAN图中描绘为连接代表每个粒子的线的线,这在其各自的连接点急剧改变过程。然而,实际上,物理学家研究的许多过程比简单的双粒子相互作用更复杂。GydF4y2Ba

计算更高的订单GydF4y2Ba
尽管有许多优点,但QFT不代表对亚原子颗粒及其相互作用的完全理解。除了一定程度的复杂程度,物理学家不可能完全描述使用QFT的量子系统。相反,他们依靠一个名为“扰动理论”的数学工具集。该理论涉及的计算从更简单的量子系统开始,该物理学家仍然可以在数学描述。然后,它们调整这些方程以更紧密地表示更复杂系统的性质。虽然扰动理论永远不能允许完美的解决方案,但它仍然足以让物理学家可以融入其中许多理论的方式来近似物理过程。GydF4y2Ba
为了描述量子系统,物理学家依赖于名为“扰动理论”的数学工具集。GydF4y2Ba
在20世纪50年代,Feyynman,沿着开创性的日本物理学家Shin'ichiròtomonaga,说明了如何在Feynman图表中表达erburation理论。他们表明,数学扰动可以由封闭的“环”表示,其中一些颗粒的路径不会与进入或离开该过程的那些连接。最终,这些线代表了短暂的“虚拟”粒子 - 不能直接观察,但是在我们观察到的颗粒相互作用中是仍然有用的。然而,对于更复杂的系统来说,只有一个扰动不足以准确地近似涉及的物理学。为了补偿,需要更高的扰动“订单”,甚至进一步增加数学复杂性。GydF4y2Ba
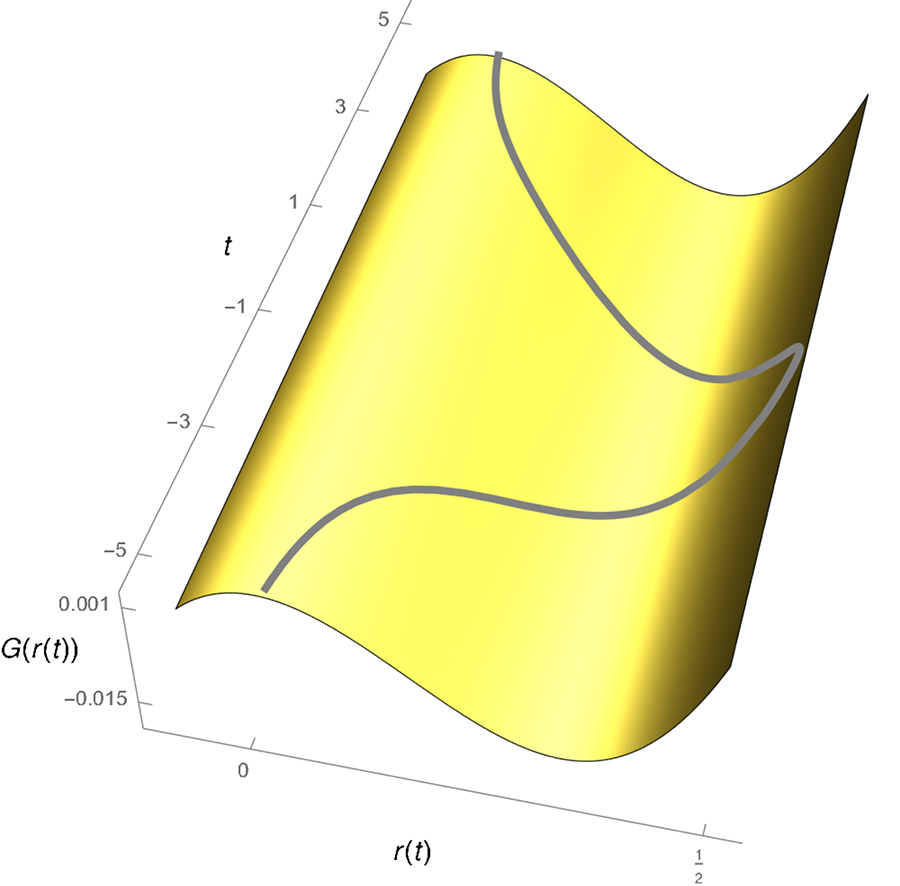
欧几里德的作用,定义为动力学和潜在能量之和的时间积分。GydF4y2Ba
收益递减GydF4y2Ba
随着理论物理学家探索更复杂的流程,他们被迫计算越来越高的扰动命令。在FEYNMAN图中,这些较高的订单显示为“循环中的循环”,其中一些路径连接到其他路径本身并不直接连接到输入或离开该过程的其他路径。对于研究人员来说,这造成了严峻的挑战:随着订单的连续更高,随后改善预测的准确性变得越来越小。最终,这导致了回报递减的法则 - 经常由工程师经历,因为对他们的设计进行了更好的调整导致更细微的改进。GydF4y2Ba
除此问题外,每个扰动所需的计算能力如何显着增加 - 拉伸目前可用的算法。迄今为止,最雄心勃勃的研究仅设法计算到20世纪70年代物理学家伯尼镍实现的六个甚至七回路订单。除此之外,甚至今天可用的最复杂的算法也达到理论阈值,也可能进一步推动。直到最近,这些限制对更准确的更准确量子过程的准确近似是否可以进行严重的疑虑。GydF4y2Ba
评估无限环GydF4y2Ba
来自Missherm的斯德哥尔摩乌尔里希·贾尼拉的联合美国 - 法国 - 意大利团队来自Missouri,Jean Zinn-Justin来自巴黎和Giorgio Parisi,Enrico Malatesta和Tommaso Rizzo从罗马,从不同的角度接近了这个问题。首先可能似乎是一个不可能的秩序,该团队考虑了几乎不可能的场景,其中在系统上进行了无限数量的扰动 - 由循环内的无限数量循环表示的系统。此时,任何进一步的扰动令都会导致精确的准确性提高,这意味着所涉及的数学已经在其当前形式的QFT允许的最佳近似下分歧。GydF4y2Ba
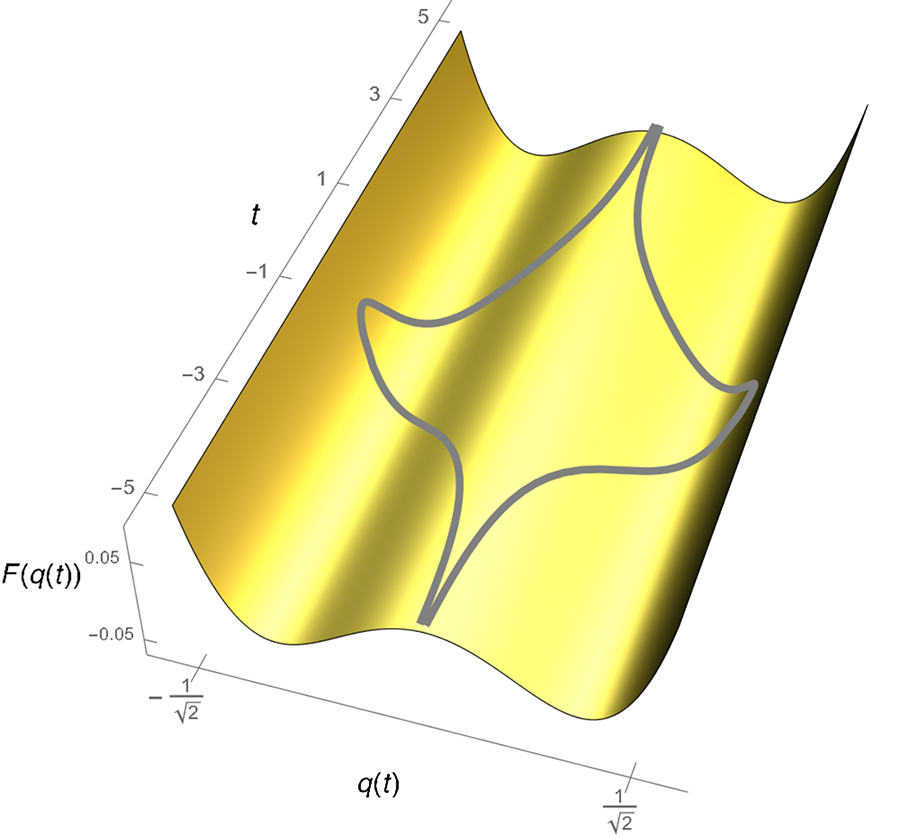
算子轨迹,由于潜力的奇偶对称性。GydF4y2Ba
尽管实现了此类计算的理论不可能,但该团队提出了本身的概念可用于克服扰动性高扰动所带来的困难。在他们以前的研究中,他的团队讨论了对高扰动命令的数学如何出现在其分歧的情况下进行了解的猜测。这些想法以QFT命名为“相关函数”的基本方面为中心,这描述了量子字段的性质如何在不同的位置变化,以及如何在古典领域分析它们 - 例如电磁场。然而,这些早期的方法呈现了进一步的困难:两者都在数学和计算能力方面。GydF4y2Ba
研究团队可以对这些较高订单的数学进行教育猜测,使他们能够精确地近似阶段转换在系统内的转换。GydF4y2Ba
重新定位群体GydF4y2Ba
根据他们之前研究的成功(部分,由Jentschura和Zinn-justin完成的工作),该团队接下来考虑了在使用这些相关性的校正时需要大量循环的Feynman图所需的改变职能。在其最新研究中,他们展示了所得数量如何被传达作为命名为“Renormalisation Group”的数学构造。这些组允许在微观和宏观尺度上系统地进行复杂物理系统中的任何变化。这种方法对于确定相变的临界指数至关重要。GydF4y2Ba
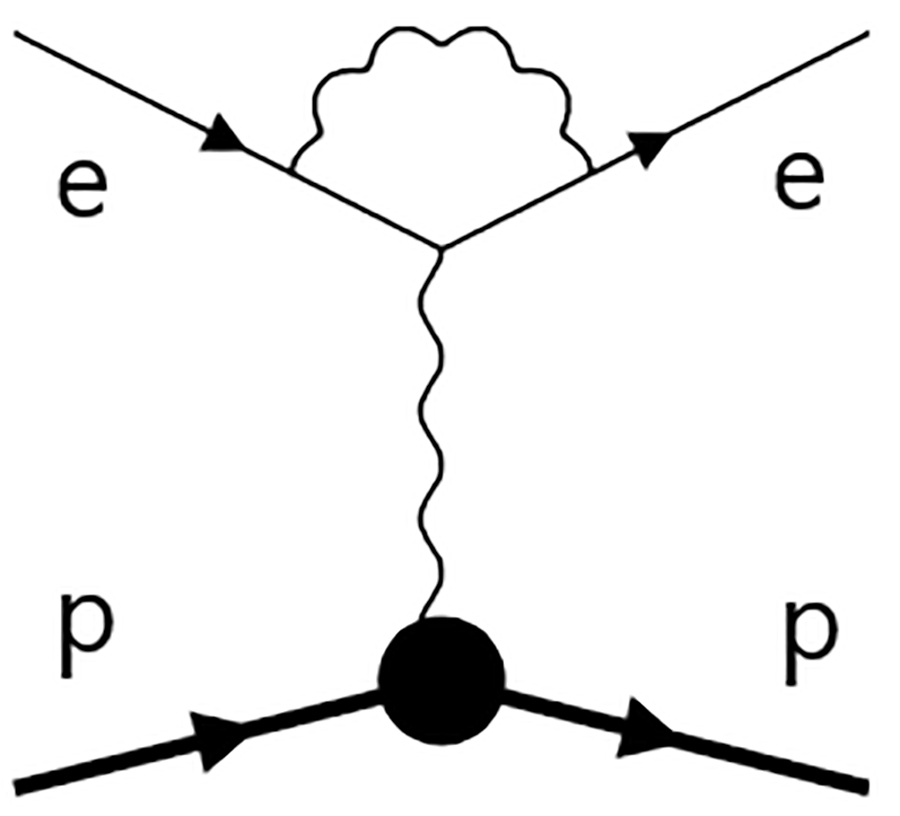
这里,该团队考虑了如何在更简化的情况下应用相关函数的相关功能,而不是他们先前调查的情况,使他们能够更好地评估其受教育的假设的后果。为了测试它们的方法,它们使用它来分析模拟的一维系统的量子颗粒,其随着温度变化而过渡到不同的相中。GydF4y2Ba
由于量子缠结现象,这种系统对研究具有高度复杂的研究,这在每个单独粒子的性质之间产生复杂的串扰腹板。反过来,它们需要大量的扰动进行准确地近似地近似。在相关功能的帮助下,研究团队可以以重新调整组的形式对这些更高的订单的数学进行教育猜测。这使它们能够精确地近似于阶段转换在系统内的转换。GydF4y2Ba
跳过繁琐的计算GydF4y2Ba
这种方法完全避免了计算使用QFT近似数学解决方案所需的每个单个扰动顺序的解决方案。相反,它允许研究人员直接向近似高订单所需的数学跳跃,只是传统扰动理论中的计算能力的一小部分。如果他们的想法得到了广泛接受的话,团队希望他们能够在理论物理学的许多分支中实现重大进展,这必须在计算能力的限制时,他们进行计算。GydF4y2Ba


通过分析重新调制组,该团队预测未来的研究可能会对高度复杂系统的性质获得前所未有的见解,包括大群缠绕量子颗粒。最终,他们得出结论,通过改善QFT的基本方面,可以克服扰动理论的预测极限。随着研究人员继续证明我们宇宙的基本属性,更精细细节,这知识很快就会进一步推进。GydF4y2Ba
个人反应GydF4y2Ba
什么激发了你进行这项研究的启发?GydF4y2Ba
使用您的方法可以更好地研究哪些系统?GydF4y2Ba

