有意识地计算无意识的偏见:二分式估值的作用
一般来说,在做任何选择时——从选择一只股票到选择一块切得很整齐的蛋糕——一个人的决定不可避免地会被他或她自己的偏见所扭曲。人们一直在潜意识中这样做,心理学领域的很多学者都写过大量关于选择偏差的文章。然而,本文提出的研究采用了不同的方法,从统计学家的角度看待这种偏差;特别地,它检查了二分估值在选择偏差中可以发挥的作用。
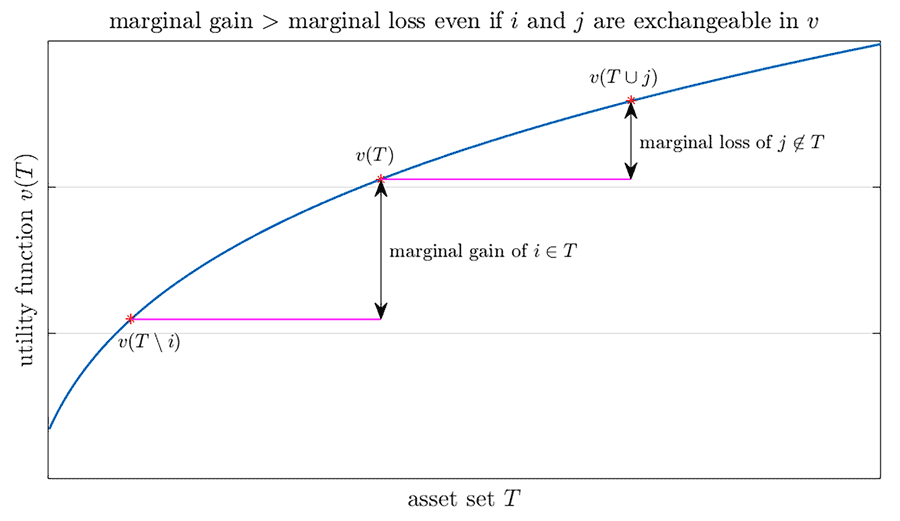
本质上,这意味着从两个不同的角度看待估值。对于决策,这归结为人们如何看待他们决策的结果。用蛋糕来打个比方,想象有人正在看一个刚被切好的蛋糕。当选择吃哪片时,人们会下意识地用边际损失或边际收益来衡量。如果他们有一块没有很多浇头的大蛋糕,他们会像一片覆盖着很多糖屑和樱桃的小蛋糕一样享受吗?此外,第一个选择者拥有先发优势,而最后一个选择者没有选择余地。

再举一个例子,考虑一个50岁的男人的年收入与学士学位的价值,我们不确定他是否拥有学士学位。根据所有权的不确定性程度,价值有以下两个方面。如果他有BD,边际收益是他当前年收入和他估计年收入之间的差,假设他没有BD,在其他条件相同的情况下。另一方面,如果他没有BD,则边际损失是假设他有BD的估计年收入与当前收入之间的差额,在其他条件相同的情况下。所有权也与决定他收入的其他因素交织在一起。
虽然这些是简单的例子,但选择偏见的概念在统计数据中具有优异。在更复杂的情况下,蛋糕切割机可能对蛋糕有多大,而且有多少人会得到一片。类似地,在选择来自许多候选者的特征到模拟和预测数据中,选择器没有关于特定特征的特征属于数据生成过程的先验知识;他或她的目的是减轻所有权不确定性。人们应通过预期的边际增益和边际损失来衡量特征,事件,财产或结果,纳入其他因素的所有权和相互依存。基本上,选择偏差被定义为边际增益与边际损失之间的预期差异。

选择偏差的作用
在他最近的论文中,“具有可变选择的应用的二分法估值理论”,国际货币基金组织(imf)的计量经济学专家胡星伟博士(Dr Xingwei Hu)决定进一步研究这种偏差在特征选择(或称为变量选择)中扮演的角色。在机器学习中,特征选择是选择相关特征(变量、预测器等)的子集用于模型构建的过程。胡博士的方法使用了博弈论(评估所有参与者联盟场景的收益)、贝叶斯理论(假设候选特征的三种等机会先验概率;先验概率指的是一个人对数据生成过程可能场景的信念),以及机制设计(将最终目标设置为评估解决方案的约束方程)。这使得他能够在广泛的建模场景中直接评估每个变量的整体性能,从而创造出一种更好的选择给定变量的方法。
根据Hu博士的说法,在模拟的线性模型中,使用四种二分值方法可以减少90%的过拟合。
这种方法有一些好处。通过对边际效应进行二分异(将其分成边际增益和边际损失)并承认模型不确定性,分析师可以概括福谢价值和Banzhaf价值。在博弈论中,诺贝尔·劳伊特劳埃德S.福利介绍的福利价值是即使他们的贡献不平等,也是在联盟中工作的几个演员的收益和成本的解决方案。它看起来将在一个人对整体成功的贡献之前所采取的组合数量是对其他人的贡献。Banzhaf值更简单,在所有可能的联盟中占据了平均边际收益。利用二分法,胡博士能够引入偏见的概念并发现Banphaf值的对称性和福音价值的不对称。对于Banzhaf值,每个玩家的偏置为零。如果支付函数平均,随着联盟规模的增长,平均,平均,递减(或增加)边缘性,福利价值具有负(或积极的)偏见。
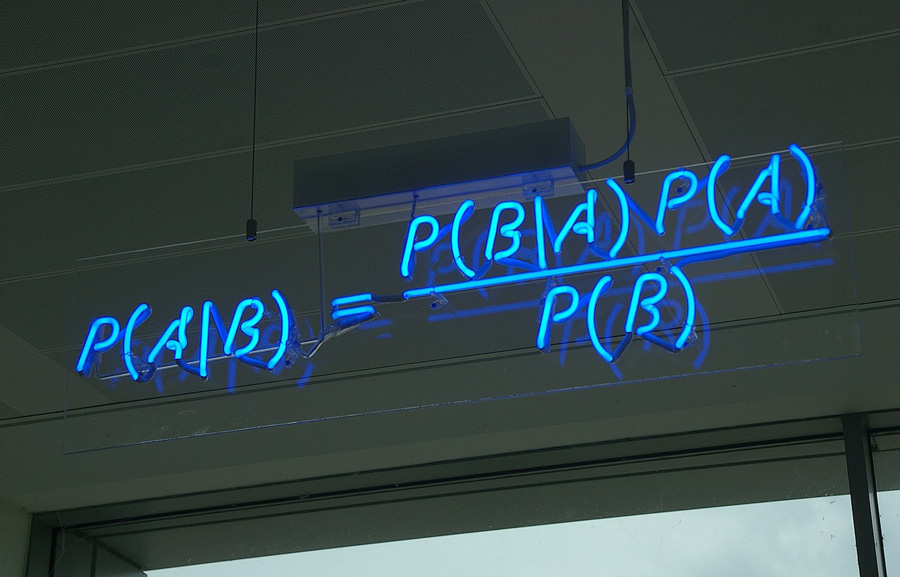
引入两个估价
从一开始,就必须认识到胡博士的工作在机器学习、统计学和计量经济学方面的应用。这意味着,通过开发沙普利值(Shapley Value,在数据建模和预测领域变得越来越流行),统计学家还可以提供解决方案,以减少行为经济学中的禀赋偏差。同时,重要的是要理解所有的数据建模都受到客观和主观不确定性的影响。
因此,在评估一般数据集时,用空白板来做这个决定是有意义的,并且假设没有关于协变量之间关系的先验知识。因此,这意味着在选择过程开始之前,人们选择一个给定变量的可能性是相同的(机会均等被凯恩斯的无差异原则正式证明了)。
这就引出了胡博士工作的重点:二分法估值。简单地说,这是一种对给定变量的二进制结果进行同等权衡的方法。例如,想象一个由12名陪审员组成的陪审团。一个特定的陪审员可能有两种关键的情况,一种是将可能失败的选票变成可能获胜的选票,另一种是将可能失败的选票变成可能获胜的选票。这种关键情况发生的可能性可以衡量陪审员的力量。这意味着当玩家观察边际收益和边际损失之间的关系时;这些可以组合起来产生一个二分值。

养老偏见
这样做的一个好处是二分值不是一个常量,它依赖于底层数据。这本身是有用的,但对统计学家来说,真正的价值在于二分值分离了边际收益和边际损失,因此可以表述并分析两者之间的偏差。用专业术语来说,“禀赋偏差”可以归结为这样一个概念:人们认为自己拥有的东西比自己不拥有的东西更有价值(即使这些东西的价值是可以交换的)。然而,当在Shapley值和Banzhaf值的背景下使用时,偏差的缓解有所改变。
胡博士的工作表明,新的选择方法可以成功地消除先动优势——一个重要的偏斜和偏见的来源。
通过Banzhaf值,所有玩家的偏差都只是零。然而,这忽略了边际效应中的不确定性。例如,想象一家正在建立一个新部门和决定谁将要头的公司。如果公司在内部完成这一目标,这意味着看他们已经雇用的候选人。因此,他们将知道这些候选人的边际生产以及对工作的兴趣程度如何。但是,如果他们去外部并雇用某人,那么有一种主观的不确定性,关于该人的效率如何。因此,在风险厌恶估值中,阳性禀赋偏差是优选的,其它物质保持不变。在外行的条款中,这是一个非常有用的案例'更好的魔鬼'。
简单地看一下沙普利值及其在建模和预测中的使用,沙普利值往往显示出大量的负禀赋偏差。这个违反直觉的问题可能会给用户带来不期望的数据推断,最终限制价值概念的使用。
因此,为了帮助更多客观估值,胡博士建议通过不均匀地加权两种二分的边际效果来系统地消除聚集体偏压,使得加权边缘增益与加权边际损失相匹配。根据胡博士的作品,使用无偏异的二分值方法的使用减少了在研究中的显着90%的过度拟合。在实际上,统计和机器学习的过度统计和机器学习模型是不准确的,试图预测数据的数据趋势,该模型对数据来说太吵了。

这一切都很重要,因为它解决了机器学习、计量经济学和统计学中的一个基本问题,特别是胡博士发现了几个广泛使用的Shapley值的新属性。通过分解预期边际损失和预期边际收益的值,统计学家可以假设一种特定类型的均等机会先验(通过机制设计,四个新的价值概念中的两个是对潜在数据生成过程的预期性能的公平分割解决方案;另一个是近似的公平分割解)。同样,无偏Shapley值可以表示为另一类二分类值的化合物。
基于这一点,可以制定新的选择方法,其中博士的工作暗示将成功地消除第一译种优势 - 这是偏斜和偏见的重要来源。如触摸,关键是如何加权这些收益和损失,这可以根据所使用的选择系统以不同的方式改变。这项工作的实际应用是有趣的,胡博士已经能够在劳动力市场中使用分析汇总的边际损失和收益,以分配雇用和失业工人之间的净利润。根据具体背景,这些想法可以应用于其他经济学,政治科学和统计领域。

个人反应
你下一步打算学什么?

